1. Kolmogorov Probability Axiom

• All of Statistics 의 Part 1 : Probability Theory 에서 다루었던 내용을 수학적으로 다룬다
• 확률론에서 Kolmogorov Probability Axiom 과 \(\sigma\)-algebra 의 중요성을 배운다

Introduction

• 확률은 불확실성(uncertainty) 을 수량화(quantify) 하기 위한 수학적인 언어
• 확률을 다루기 위해선 확률공간 (Probability space) 이란 용어를 소개한다
  • 표본공간(Sample space) \(\Omega\) 는 가능한 결과(outcome) \( \omega \) 들의 집합
  • \( \omega \) 는 표본결과(sample outcome), 실현(realization), 원소(element) 등 여러가지 용어로 불린다
  • \( \omega \) 의 일부를 모은 \( \Omega \) 의 부분집합들을 사건(Events) 이라 부른다
• 확률(probability) 은 사건들 위에 정의되는 함수라 볼 수 있다. 그런데 주의할 점은 모든 사건들에 확률이 정의되는 것은 아니다!

Bertrand Paradox

죠셉 베르트랑(Joseph Bertrand) 은 1889년 그의 저서 Calcul des probabilités 에서 확률의 기초에 관한 역설을 소개했다

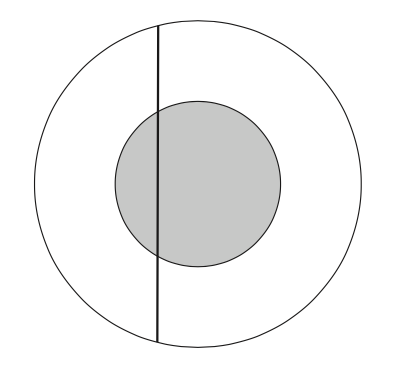
Take a circle of radius 2 in the plane and choose a chord of this circle at "random". What is the probability this chord intersects the concentric circle of radius 1 ?

• 문제 : 반지름이 2인 원 안에 중심이 같고 반지름이 1인 원이 있다. 반지름이 2인 원 내부에서 임의로 직선을 하나 그었을 때, 이 직선이 반지름이 1인 원을 지날 확률은 얼마인가?
  • 답안 1 : 그어진 직선이 내부 원을 지나려면 해당 직선의 중점이 반지름이 1인 원 안에 있어야 한다. 그러므로 두 원의 넓이의 비율인 \(\frac{\pi}{4\pi}=\frac{1}{4}\) 이 답이다
  • 답안 2 : 직선과 원의 중심사이의 거리가 1보다 작아야먄 내부 원을 지난다. 점과 직선 사이의 거리의 가능한 범위는 0 부터 2 사이이다. 그러므로 \(\frac{1}{2}\) 이 답이다
  • 답안 3 : 외부 원과 직선이 만나는 교점에서 원의 중심으로 보조선을 그어보자 (교점은 두 개지만 어느 것이든 상관없다). 이 때 보조선과 직선 사이의 각도가 \(\frac{\pi}{6}\) 이하이면 내부 원을 지나게 되므로 \(\frac{2 \times \frac{\pi}{6}}{ \pi} = \frac{1}{3}\) 이 답이다

• 이 역설에서 서로 다른 답이 나오는 이유는 문제에서 임의로(random) 라는 상황을 명확하게 기술하지 않았기 때문이다. 확률적인 현상을 기술하려면 근본적으로 현상의 구조(mechanism) 에 대한 명확한 설정 또는 가설(Hypothesis)이 필요하다

• 현대 확률론에서는 베르트랑의 역설을 측도론(Measure Theory) 을 기초로 한 콜모고로프의 확률공리 (Kolmogorov Probability Axiom) 를 도입함으로써 해결한다

\(\sigma\)-algebra

• Kolmogorov Axiom 을 소개하려면 우선 \(\sigma\)-algebra (또는 \(\sigma\)-field) 를 알아야 한다

• 여기서 \(\sigma\) 는 표준편차나 분산(variance)과는 관련이 없고, 합(sum)을 의미하는 \(\Sigma\) 기호와 관련있다. 이는 밑에서 소개할 Kolmogorov Axiom 중 세번째와 관련 있다

• 사건들의 전체집합인 표본공간(Sample space) 을 \(\Omega\) 로 표기하자. \(\Omega\) 의 모든 부분집합들의 모임을 \(2^{\Omega}\) (이를 멱집합(Power set) 이라 한다) 라 할 때, 다음 세 가지 조건을 만족하는 \(\mathcal{F} \subset 2^{\Omega}\) 을 \(\sigma\)-algebra 이라 정의한다
  1. 표본공간은 항상 포함한다 : \(\Omega \in \mathcal{F}\)
  2. 여집합은 항상 포함한다 : If \(A \in \mathcal{F}\) then \(A^{c} \in \mathcal{F}\)
  3. 가산합집합(countable union) 은 항상 포함한다 : If \(A_{1},A_{2},\ldots \in \mathcal{F}\) then \(\bigcup_{i=1}^{\infty}A_{i}\in\mathcal{F}\)
• 위의 세 가지 조건을 유심히 살펴보면 \(\sigma\)-algebra 는 집합 연산(set operation) 에 대해 닫혀있는 부분집합들의 모임이다.
  • 교집합(intersection) : \( A, B\in\mathcal{F} \) 라고 하자. 2번에 의해 \(A^{c}, B^{c}\in\mathcal{F} \) 이다. 따라서 3번에 의해 \( A^{c} \cup B^{c} \in\mathcal{F} \) 이다. 그러므로 다시 2번과 De Morgan 의 법칙에 의해 \( A \cap B = (A^{c} \cup B^{c} )^{c} \in\mathcal{F} \) 이다
  • 차집합(substraction) : \( A, B\in\mathcal{F} \) 라고 하자. 2번에 의해 \( B^{c}\in\mathcal{F} \) 이다. \( A \setminus B = A \cap B^{c} \) 이므로 위의 교집합에 대한 논리에 의해 차집합 연산에 대해서도 닫혀있다.
  • 가산교집합(countable intersection) : \(A_{1},A_{2},\ldots \in\mathcal{F}\) 라고 하자. 2번에 의해 \(A_{1}^{c}, A_{2}^{c},\ldots \in\mathcal{F} \) 이다. 그러므로 3번에 의해 \( \bigcup_{i=1}^{\infty}A_{i}^{c}\in\mathcal{F} \) 이다. 마지막으로 De Morgan 의 법칙과 2번에 의해

• \( \sigma \)-algebra 가 집합 연산에 대해 닫혀있다는 것은 확률론에서 어떤 의미를 가질까? 밑에서 다시 보겠지만 확률이란 \( \Omega \) 의 부분집합들 위에 정의된 집합함수(set function) 로써 임의의 집합을 \( [0,1] \) 위의 실수(real number)로 보내는 함수이다. 우리는 확률을 계산할 때 체계적이고 일관성 있길 바란다. 가령 날씨예측을 하는 경우, 어떤 연구자가 내일 비가 올 확률이 25% 인데 이틀 연속 비가 올 확률이 50% 라는 분석을 내놨다고 하자. 전자의 사건이 후자를 포함하는데 확률이 더 낮다는 건 논리적으로 이해할 수 없는 것이다. . 이는 결국 “어떤 사건들에 대해 확률 계산이 가능한가?” 라는 질문으로 연결된다. 다시 말해 \( \sigma \)-algebra 는 아래와 같은 확률 연산들이 가능한 닫힌체계(closed system)로 해석할 수 있다.

ex) 동전 던지기를 예를 들어보자. 동전을 한 번만 던지는 경우를 생각한다 : \(\Omega = \{H,T \} \)

• 우선 전체집합을 포함해야 하므로 \(\Omega \in \mathcal{F}\) 이다
  • 2번 조건인 여집합에 대해 닫혀있으려면 \(\Omega^{c}=\emptyset \in\mathcal{F}\). 여기까지 완성해도 \(\sigma\)-algebra 의 요건을 만족한다 (이를 minimal \(\sigma\)-algebra 이라 부른다)

• 동전이 앞이 나오는 사건 \(H\) 을 포함한다고 하자 : \(\{H\}\in\mathcal{F}\) (주의 : \(H\in\mathcal{F}\) 이 아니다)
  • 역시 여집합을 포함해야 하므로 \(\Omega\setminus\{H\} = \{T\}\in\mathcal{F}\). 이 경우 \(2^{\Omega}\) 와 같게 된다 (이를 maximal \(\sigma\)-algebra 이라 부른다)

ex) 동전을 두 번 던져보자 : \(\Omega = \{HH, HT, TH, TT\}\)

• 마찬가지로 minimal \(\sigma\)-algebra 는 \({\Omega,\emptyset}\) 이고 maximal \(\sigma\)-algebra 는 \(2^{\Omega}\) 이다

• 동전이 두 번 연속 앞이 나오는 사건과 뒤가 나오는 사건을 포함한다고 하자 : \(\{HH\}, \{TT\}\in\mathcal{F}\)

  • 여집합이 포함되어야 하므로 \(\Omega\setminus\{HH\} = \{HT, TH, TT\}\in\mathcal{F}\) 이고 \(\Omega\setminus\{TT\} = \{HH,HT, TH\}\in\mathcal{F}\) 이다
  • 합집합이 포함되어야 하므로 \(\{HH\}\cup\{TT\} = \{HH,TT\}\in\mathcal{F}\)
  • 다시 \(\{HH, TT\}\) 의 여집합이 포함되어야 하므로 \(\{HT, TH\}\in\mathcal{F}\). 여기까지 만든 \(\mathcal{F}\) 는 \(\sigma\)-algebra 의 조건을 만족하지만 \(\{HT\},\{TH\}\) 라는 단독 사건들에 대한 정보를 포함하지 않는다

• 이런식으로 만들 수 있는 \(\sigma\)-algebra 의 개수는 총 18개이다

• \(\sigma\)-algebra 는 관찰가능한 정보집합(information sets) 또는 측정가능한 집합(measurable sets) 들의 모임(class)으로 해석한다

• 시간(time)과 공간(spatial)에 따라 다르게 관찰되는 정보집합들로 다양한 \(\sigma\)-algebra 을 구성할 수 있다. 이에 대한 구체적인 논의는 확률과정 (stochastic process) 이나 조건부 기대값 (conditional expectation) 에서 다룬다

Kolmogorov Probability Axiom

• Kolmogorov 는 그의 저서 Foundations of the Theory of Probability (1933) 에서 현대확률론의 공리들을 소개하였다

• 표본공간 \(\Omega\) 와 그 위에 정의된 \(\sigma\)-algebra \(\mathcal{F}\) 가 주어져 있다고 하자. 이 때 \(\mathbb{P}\) 는 \(\mathcal{F}\to[0,1]\) 인 함수로서 다음의 Kolmogorov Probability Axiom 을 만족하면 확률측도(Probability measure) 또는 간단히 확률 이라 부른다.

  • Axiom 1. 어떤 사건 \( A \in\mathcal{F} \) 이든 \(\mathbb{P}(A) \geq 0\)
  • Axiom 2. \(\mathbb{P}(\Omega) = 1\)
  • Axiom 3. 서로 겹치지 않는 (disjoint) 사건들 \(A_{1}, A_{2},\ldots \in\mathcal{F} \) 에 대해

• 표본공간 \(\Omega\), \(\sigma\)-algebra \(\mathcal{F}\), 확률측도 \(\mathbb{P}\) 세 가지가 모두 잘 정의되어 있을 때 \((\Omega,\mathcal{F},\mathbb{P})\) 를 확률공간(Probability space) 이라 부른다

• 위에서 소개한 Bertrand paradox 에서 표본공간 \(\Omega\) 는 가능한 직선들의 집합으로 공통이지만 \(\sigma\)-algebra 는 서로 다르다
  • 답안 1은 중점의 좌표 \( (x,y) \) 가 같은 직선들의 집합 으로 \(\sigma\)-algebra 를 구성한다
  • 답안 2는 직선과 원의 중심 사이의 거리 \( d \) 가 같은 직선들의 집합 으로 \(\sigma\)-algebra 를 구성한다 : \( 0 \leq d \leq 2 \)
  • 답안 3은 보조선과 직선의 각도 \( \theta \) 가 같은 직선들의 집합 으로 \(\sigma\)-algebra 를 구성한다 : \( 0\leq \theta \leq \pi \)
  • 각 \(\sigma\)-algebra 에 균등분포(uniform distribution) 를 정의하면 위와 같이 서로 다른 답이 나오는 것이다
• 왜 \(2^{\Omega}\) 가 아니라 복잡하게 \(\sigma\)-algebra 를 생각하는 걸까?
  • 사실 표본공간 \(\Omega\) 의 원소의 개수가 유한(finite)하면 상관없다. 문제는 표본공간이 무한집합인 경우에 발생한다. 위의 세 공리를 동시에 만족 못하는 문제 가 생기기 때문이다 (수학적으로 이 문제는 선택공리(Axiom of choice) 때문에 발생한다)